Futures Rollover
Introduction to Futures
Futures are a form of a contract drawn up between two parties to purchase or sell a quantity of an underlying asset at a specified date in the future. This date is known as the delivery or expiration. When this date is reached, the buyer must deliver the physical underlying (or cash equivalent) to the seller for the price agreed at the contract formation date.
In practice, futures are traded on exchanges for standardised quantities and qualities of the underlying. The prices are marked to market every day. Futures are incredibly liquid and are used heavily for speculative purposes. While futures were often utilised to hedge agricultural or industrial goods’ prices, a futures contract can be formed on any tangible or intangible underlying such as stock indices, interest rates of foreign exchange values.
The main difference between a futures contract and equity ownership is the fact that a futures contract has a limited window of availability by virtue of the expiration date. At any one instant, there will be a variety of futures contracts on the same underlying all with varying dates of expiry. The contract with the nearest date of expiry is known as the near contract.
Some basics about Futures trading
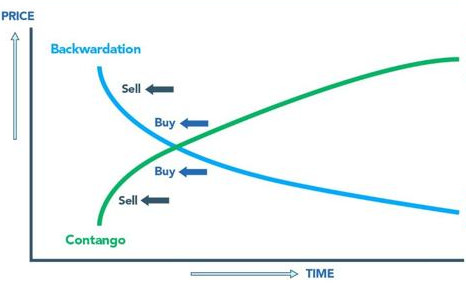
Contango vs Backwardation. (SeekingAlpha 2017)
For our purposes, we will refer to front and back contracts, where the front contract is the first Futures due for expiry, while the back contract matures later by a particular frequency (often one or three months after the front contract).
In the context of comparing the prices between two subsequent Futures, a higher price in the back contract is referred to as contango, while we speak of backwardation in case of the opposite price relationship.
Tick size refers to the smallest possible price movement, and the tick value is the loss or gain incurred by that movement.
So first of all, we have to ask, why there is a difference in the price in subsequent Futures contracts at all?
One way to gain an understanding of this is to follow the close link between the Futures contract and underlying, and at the same time acknowledge that, — given an arbitrage free world — a holding, whether in the underlying or the Futures, will yield exactly in the same payoffs for the investor.
So more precisely, the cost of holding the underlying until the next respective expiration date, determines the gap between two contracts. Depending on the market, those influence factors can be repo rates, dividends, storage costs, etc.
The main difficulty with trying to generate a continuous contract from the underlying contracts with varying deliveries is that the contracts do not often trade at the same prices. Thus situations arise where they do not provide a smooth splice from one to the next. This is due to contango and backwardation effects. There are various approaches to tackling this problem, which we now discuss.
Forming a Continuous Futures Contract
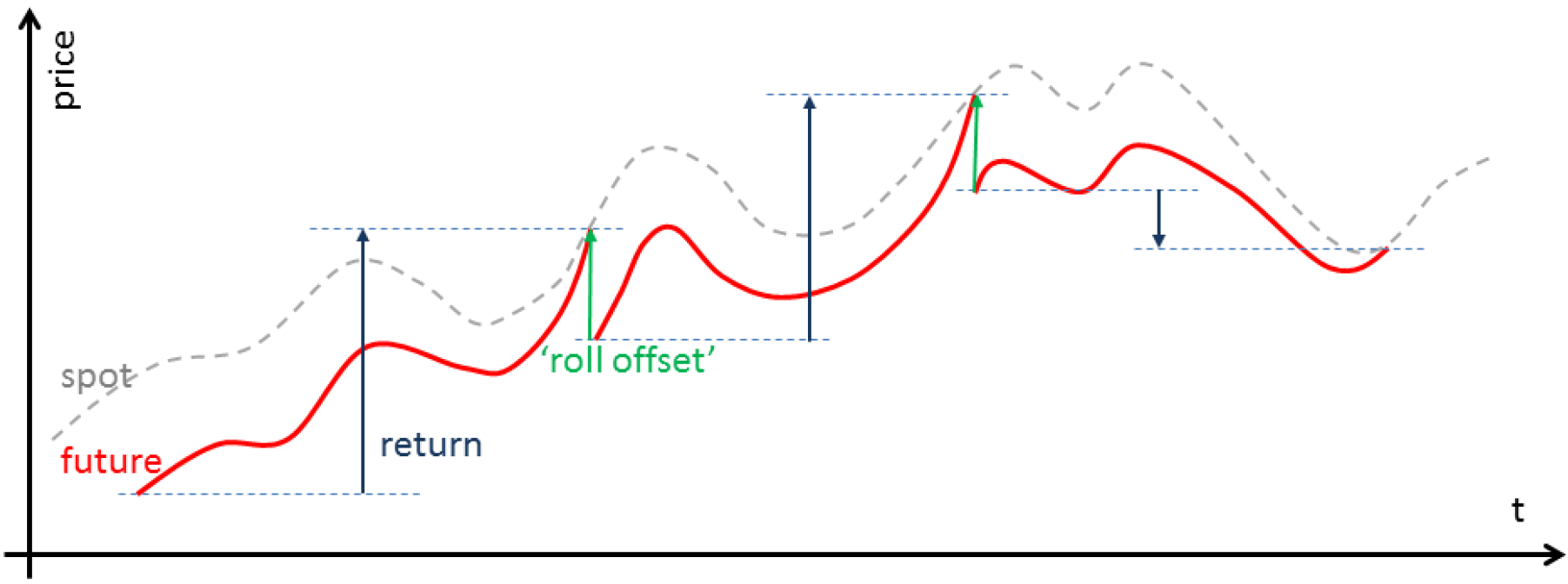
Visual intuition of rolling procedure. (Winton 2014)
Unfortunately, there is no single “standard” method for joining futures contracts together in the financial industry. Ultimately the method chosen will depend heavily upon the strategy employing the contracts and the method of execution. Despite the fact that no single method exists there are some common approaches:
Splicing contracts together with no adjustments
This is typically done already by market data providers like Bloomberg. We will (possibly) end up in a price jump on the day when contracts are switched. In case trading signals are extracted from those series, we rely on a mix of inputs from both contracts potentially yielding a biased result as the price jump is inherited in the calculations. We also receive a distorted picture with regards to backtesting the PnL of any strategy relying on such a time series.
Splicing contracts together with forward or backward adjustments (“Panama Adjustment”)
This method alleviates the “gap” across multiple contracts by shifting each contract such that the individual deliveries join in a smooth manner to the adjacent contracts. Thus the open/close across the prior contracts at expiry matches up.
The Panama method’s key problem includes the introduction of a trend bias, which will introduce a large drift to the prices. This can lead to negative data for sufficiently historical contracts. In addition, there is a loss of the relative price differences due to an absolute shift in values. This means that returns are complicated to calculate (or just plain incorrect).
Proportional Adjustment
The Proportionality Adjustment approach is similar to the adjustment methodology of handling stock splits in equities. Rather than taking an absolute shift in the successive contracts, the ratio of the older settle (close) price to the newer open price is used to proportionally adjust the prices of historical contracts. This allows a continuous stream without an interruption of the calculation of percentage returns.
The main issue with the proportional adjustment is that any trading strategies reliant on an absolute price level will also have to be similarly adjusted in order to execute the correct signal. This is a problematic and error-prone process. Thus this type of continuous stream is often only useful for summary statistical analysis, as opposed to direct backtesting research.
Continuously adjusting the contracts over time (“Perpetual Method”)
The essence of this approach is to create a continuous contract of successive contracts by taking a linearly weighted proportion of each contract over a number of days to ensure a smoother transition between each. The problem with the rollover method is that it requires trading on all five days, which can increase transaction costs.
Base Implementation
Contract Specific Implementations
Example
# Importing packages
from arbitragelab.util.rollers import *
# Getting the dataframe with time series of continous future prices.
data = pd.read_csv('X_FILE_PATH.csv', index_col=0, parse_dates = [0])
# Fit corresponding roller and retrieve gaps.
wti_roller = CrudeOilFutureRoller().fit(data)
wti_gaps = wti_roller.transform()
# Store forward rolled series.
rolled_contract = cl_df['PX_LAST'] - wti_gaps
# Sometimes rolled contracts dip into negative territory. This
# can cause problems when used for ml models, thus there is the
# ability to use the parameter 'handle_negative_roll', which
# will process the price data into positive returns data.
non_negative_contract = wti_roller.transform(handle_negative_roll=True)
# The diagnostic summary is a helper function to help the user
# easily double-check expiration dates and their respective gap
# calculations.
wti_diag_frame = wti_roller.diagnostic_summary()
wti_diag_frame.head(10)
Research Notebooks
The following research notebook can be used to better understand the implementation described above.
Futures Rollover - showcases the use of various rollers on specific contracts.