Utility Modules
We also included a few functionalities that are often used for copula-based trading strategies in the copula_approach
module listed below:
Empirical cumulative distribution function (ECDF) with linear interpolation.
Quick pairs selection using Kendall’s \(\tau\), Spearman’s \(\rho\) and Euclidean distance (for normalized prices).
ECDF
ECDF by its name, is a non-parametric estimation on a random variables cumulative distribution function. CDF maps a datapoint to its quantile in \([0, 1]\). If a CDF is chosen correctly, the data after mapping should be distributed uniformly in \([0, 1]\).
In literatures the ECDF is generally constructed from a dataset \(\mathbf{x} = (x_1, x_2, \dots x_n)\) as
where \(|| \cdot ||\) is the cardinality, or the number of elements in the set for a finite set.
This is implemented already in ECDF() from statsmodels.distributions.empirical_distribution.
Implementation
Back end module that handles maximum likelihood related copula calculations.
Functions include:
Finding (marginal) cumulative distribution function from data.
Finding empirical cumulative distribution function from data with linear interpolation.
Maximum likelihood estimation of theta_hat (empirical theta) from data.
Calculating the sum log-likelihood given a copula and data.
Calculating SIC (Schwarz information criterion).
Calculating AIC (Akaike information criterion).
Calculating HQIC (Hannan-Quinn information criterion).
Fitting Student-t Copula.
SCAD penalty functions.
Adjust weights for mixed copulas for normality.
For more information about the SCAD penalty functions on fitting mixed copulas, please refer to Cai, Z. and Wang, X., 2014. Selection of mixed copula model via penalized likelihood. Journal of the American Statistical Association, 109(506), pp.788-801.
- construct_ecdf_lin(train_data: array, upper_bound: float = 0.99999, lower_bound: float = 1e-05) Callable
Construct an empirical cumulative density function with linear interpolation between data points.
The function it returns agrees with the ECDF function from statsmodels in values, but also applies linear interpolation to fill the gap. Features include: Allowing training data to have nan values; Allowing the cumulative density output to have an upper and lower bound, to avoid singularities in some applications with probability 0 or 1.
- Parameters:
train_data – (np.array) The data to train the output ecdf function.
upper_bound – (float) The upper bound value for the returned ecdf function.
lower_bound – (float) The lower bound value for the returned ecdf function.
- Returns:
(Callable) The constructed ecdf function.
Example
# Importing libratries and data
from arbitragelab.copula_approach.copula_calculation import construct_ecdf_lin
import pandas as pd
prices = pd.read_csv('FILE_PATH' + 'AAPL_MSFT_prices.csv').set_index('Date').dropna()
# Training and testing split
training_len = int(len(prices) * 0.7)
prices_train = prices.iloc[:training_len, :]
prices_test = prices.iloc[training_len:, :]
# Construct ECDF on training set
ecdf_aapl = construct_ecdf_lin(prices_train['AAPL'])
# Apply the trained ECDF on testing set
quantile_aapl = prices_test['AAPL'].map(ecdf_aapl)
Quick Pairs Selection
We build the class PairsSelector that selects potential pairs for copula-based trading strategies.
Methods include Spearman’s rho, Kendall’s tau and Euclidean distance on normalized prices.
Those methods are relatively quick to perform and are widely used in literature for copula-based pairs trading framework.
For more sophisticated ML-based pairs selection methods, please refer to arbitragelab.ml_approach.
Comments
Kendall’s tau and Spearman’s rho are rank-based values. Thus they are non-parametric. Kendall’s tau’s computation complexity is \(O(N^2)\) and Spearman’s rho is \(O(N \log N)\). The pairs selected by \(\tau\) and \(\rho\) generally do not differ much. However, Kendall’s tau is more stable, and suffers less from outliers.
Euclidean distance is also used commonly in literatures. The pairs selected in general do not coincide with the pairs selected by \(\tau\) and \(\rho\). However, we found it not coping with copula-based strategies very well based on our backtests.
Pearson’s correlation is not included here due to its parametric approach, and assumption on normality of the underlyings.
To illustrate their differences further, here we conduct a quick run on adjusted closing prices on Dow stocks from beginning of 2011 to end of 2019:
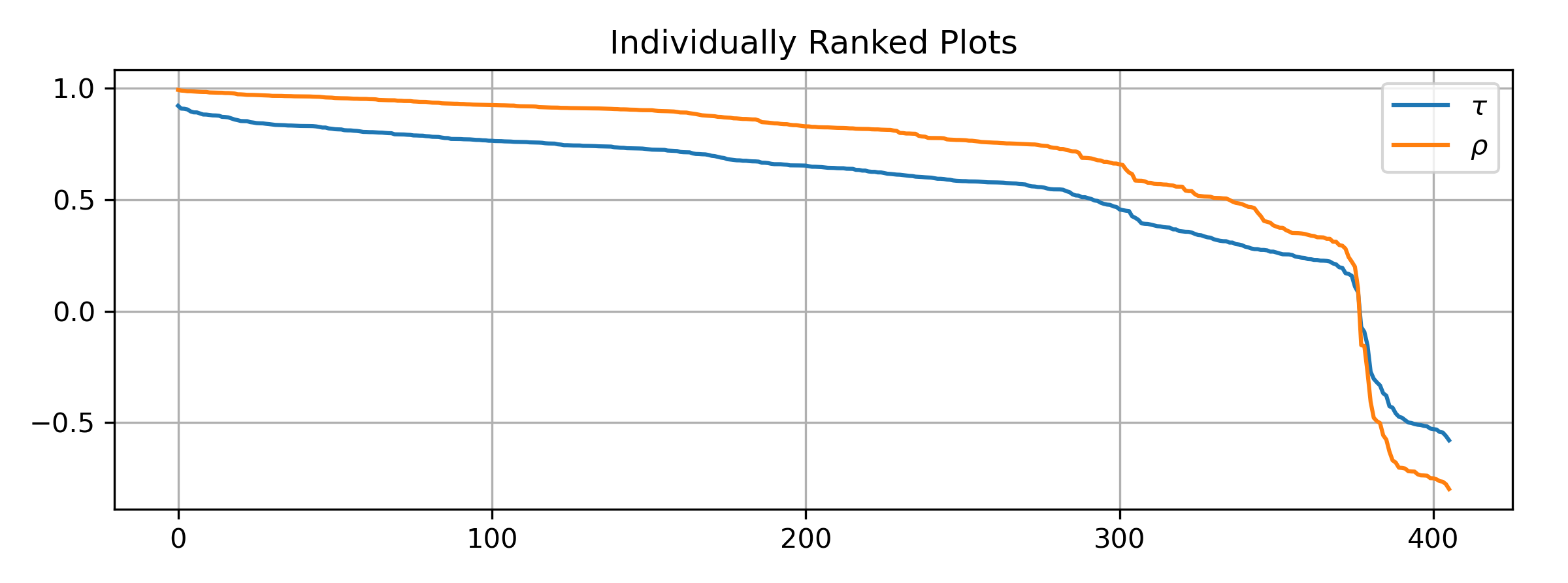
The plots are \(\tau\) and \(\rho\) scores individually for all available pairs. Value-wise, \(\tau\) is smaller than \(\rho\) in terms of absolute value.
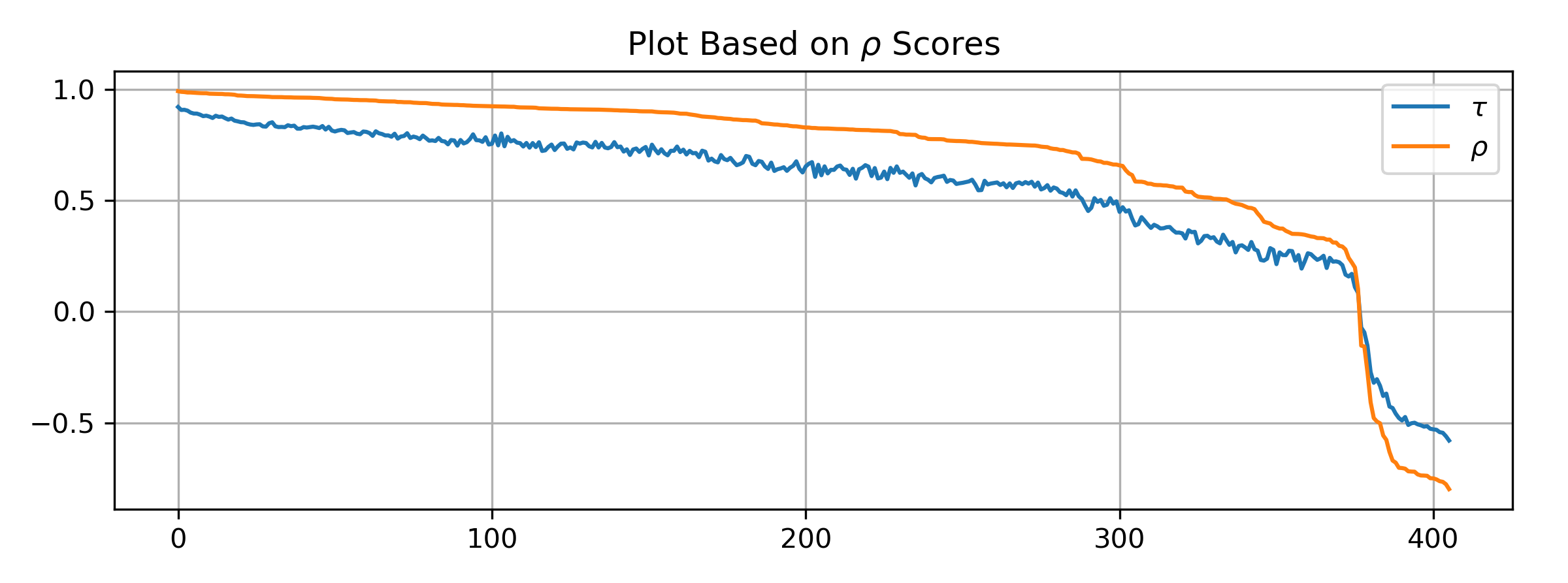
We plot \(\tau\) and \(\rho\) for all pairs, but the sequence is based on \(\rho\).
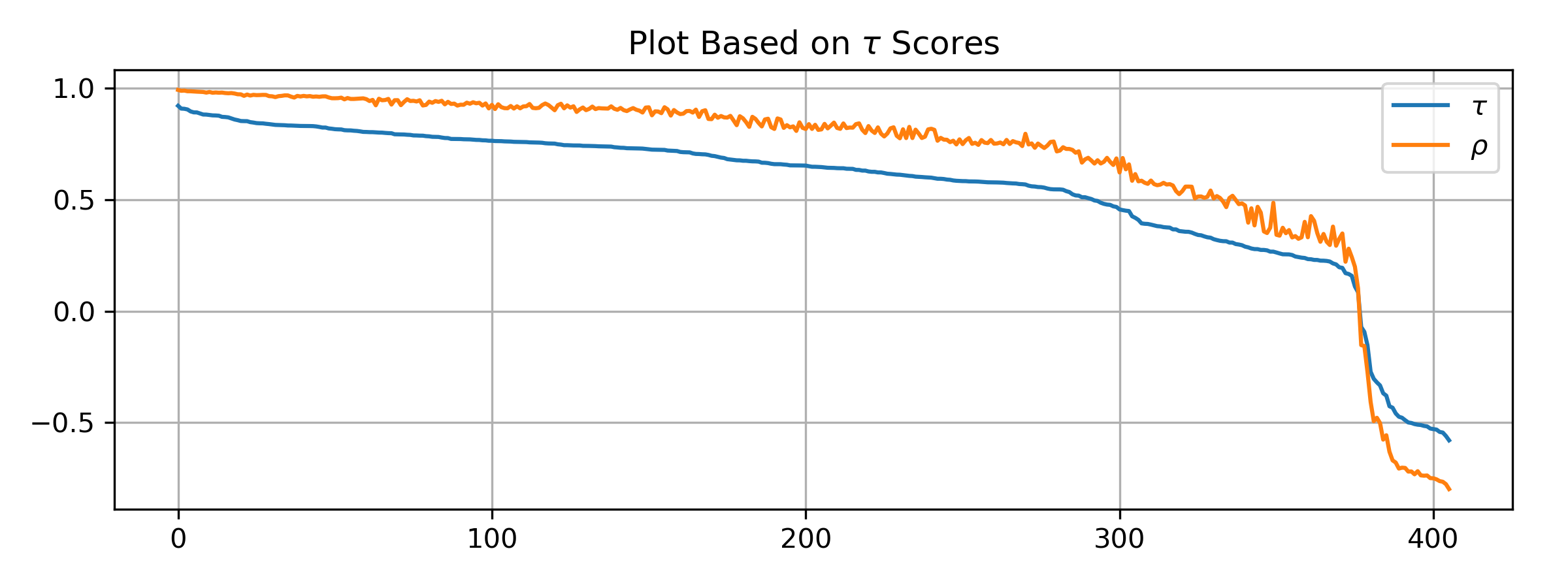
We plot \(\tau\) and \(\rho\) for all pairs, but the sequence is based on \(\tau\). We can see that \(\rho\) is a bit less stable, with slightly larger jumps.
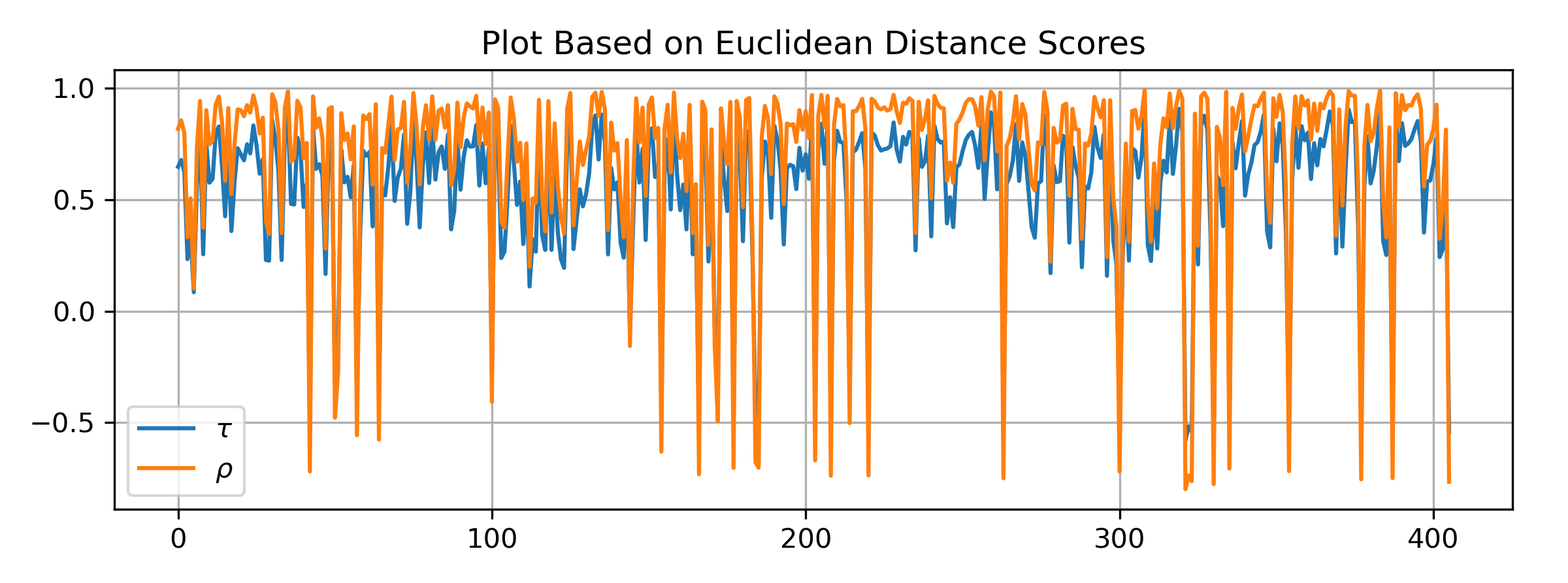
Now we plot \(\tau\) and \(\rho\) for all pairs, but the sequence is based on Euclidean distance. We can see that the Euclidean distance result do not agree with \(\tau\) and \(\rho\), also \(\tau\) is a bit more stable than \(\rho\).
Below are the top pairs normalized prices plot (cumulative return) selected by Euclidean distance and Kendall’s tau respectively. They clearly demonstrate what each method aims to capture.
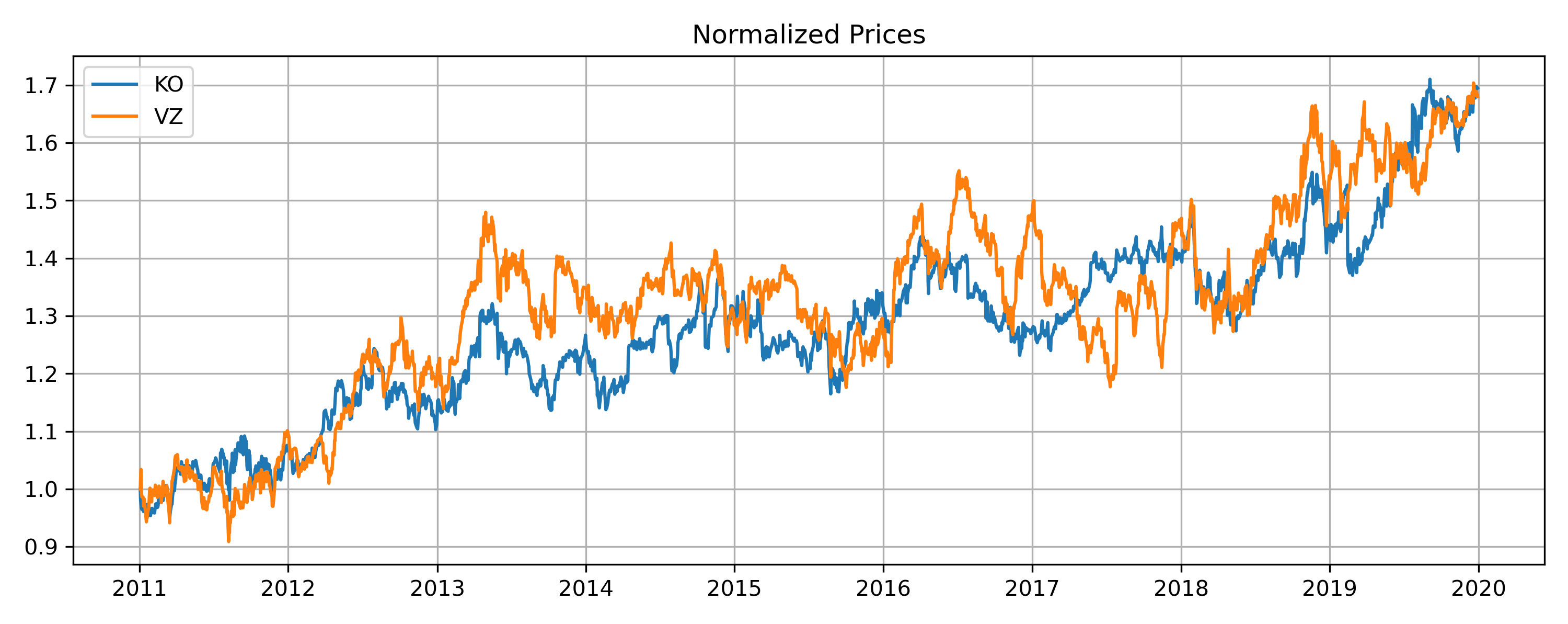
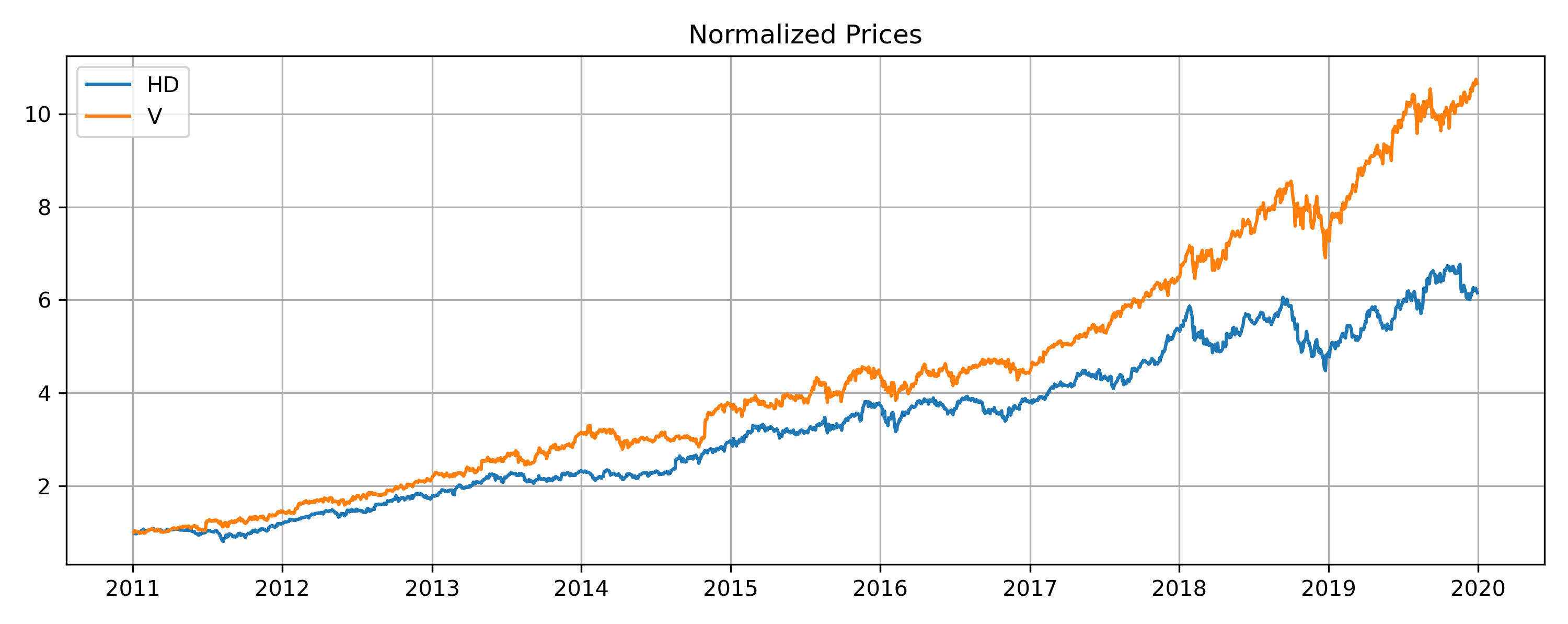
It might make more sense to look at the quantile plot for the HD-V pair selected by Kendall’s tau.
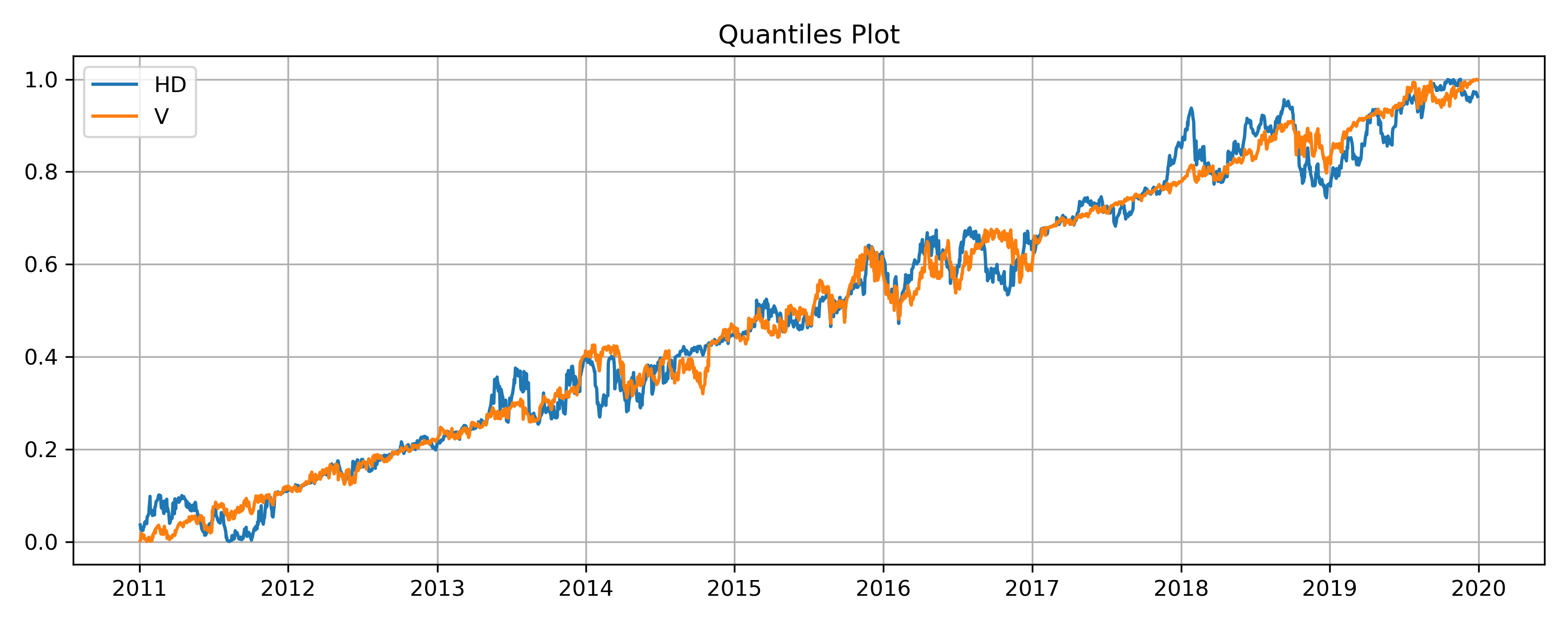
Implementation
Module for implementing some quick pairs selection algorithms for copula-based strategies.
- class PairsSelector
The class that quickly select pairs for copula-based trading strategies.
This class selects potential pairs for copula-based trading strategies. Methods include Spearman’s rho, Kendall’s tau and Euclidean distance on normalized prices. Those methods are relatively quick to perform and is generally used in literature for copula-based pairs trading framework. For more sophisticated ML based pairs selection methods, please refer to
arbitragelab.ml_approach.- rank_pairs(stocks_universe: DataFrame, method: str = 'kendall tau', nan_option: str | None = 'forward fill', keep_num_pairs: int | None = None) Series
Rank all pairs from the stocks universe by a given method.
method choices are ‘spearman rho’, ‘kendall tau’, ‘euc distance’. nan_options choices are ‘backward fill’, ‘linear interp’, None. keep_num_pairs choices are all integers not greater than the number of all available pairs. None Means keeping all pairs.
Spearman’s rho is calculated faster, however the performance suffers from outliers and tied ranks when compared to Kendall’s tau. Euclidean distance is calculated based on a pair’s cumulative return (normalized prices). User should keep in mind that Spearman’s rho and Kendall’s tau will generally give similar results but the top pairs may still drift away in terms of normalized prices.
Note: ALL NaN values need to be filled, otherwise you will likely get the scores all in NaN value. We suggest ‘forward fill’ to avoid look-ahead bias. User should be aware that ‘linear interp’ will linearly interpolate the NaN value and will thus introduce look-ahead bias. This method will internally fill the NaN values. Also the very first row of data cannot have NaN values.
- Parameters:
stocks_universe – (pd.DataFrame) The stocks universe to be analyzed. Require no multi-indexing for columns.
method – (pd.DataFrame) Optional. The method to pick pairs. One can choose from [‘spearman rho’, ‘kendall tau’, ‘euc distance’] for Spearman’s rho, Kendall’s tau and Euclidean distance. Defaults to ‘kendall tau’.
nan_option – (Union[str, None]) Optional. The method to fill NaN value. one can choose from [‘forward fill’, ‘linear interp’, None]. Defaults to ‘forward fill’.
keep_num_pairs – (Union[int, None]) Optional. The number of top ranking pairs to keep. Defaults to None, which means all pairs will be returned.
- Returns:
(pd.Series) The selected pairs ranked descending in their scores (top ‘correlated’ pairs on the top).
Example
# Importing libratries and data
from arbitragelab.copula_approach.pairs_selection import PairsSelector
import pandas as pd
stocks_universe = pd.read_csv('FILE_PATH' + 'SP500_2010_2018.csv').set_index('Date').dropna()
# Training and testing split
training_len = int(len(stocks_universe) * 0.7)
prices_train = stocks_universe.iloc[:training_len, :]
prices_test = stocks_universe.iloc[training_len:, :]
# Rank pairs from training set
PS = PairsSelector()
scores_tau = PS.rank_pairs(prices_train, method='kendall tau', keep_num_pairs=1000)
scores_rho = PS.rank_pairs(prices_train, method='spearman rho', keep_num_pairs=1000)
scores_dis = PS.rank_pairs(prices_train, method='euc distance', keep_num_pairs=1000)
Comments
Note that the approach above is a step function. Suppose we train an ECDF on some training data, for example \(\mathbf{x}_{train} = (0, 1, 3, 2, 4)\), then \(\hat{F^{-1}}(0) = \hat{F^{-1}}(0.99) = 0.2\), and \(\hat{F^{-1}}(-0.01) = 0\). This might cause issues if the data set is not large enough, and particularly troublesome where there is not enough datapoints at certain regions of the distribution. When working with copula-based strategies one essentially aims to capture relative mispricings, which is sparse in nature. Moreover, the original ECDF may yield 0 and/or 1, which will be considered edge cases for some copula calculations and we generally want to avoid it by mapping \([0, 1]\) back to \([\varepsilon, 1-\varepsilon]\) for some small positive number \(\varepsilon\).
Note
No, we are not being lazy here. Yes, we can technically adjust the calculations to allow infinities, but what if the infinity shows up when one uses a max likelihood fit? With real world data this happens more often than one might expect.
Therefore, we built our own ECDF to address the above concerns, and for all places in the module we use our own ECDF constructed by
copula_calculation.construct_ecdf_lin().The plot of ECDF vs. our ecdf. The max on the training data is \(14\), the min is \(2.2\). We made the \(\varepsilon\) for upper and lower bound much larger on our ecdf for visual effect.